Qual é o coeficiente de correlação?
O coeficiente de correlação é usado para determinar o quão forte é a relação entre duas variáveis e seus valores podem variar de -1,0 a 1,0, onde -1,0 representa a correlação negativa e +1,0 representa a relação positiva. Ele considera os movimentos relativos nas variáveis e, em seguida, define se há alguma relação entre elas.
Fórmula do Coeficiente de Correlação
r = n (Σxy) - Σx Σy / √ (n * (Σx 2 - (Σx) 2 )) * (* N (Σy 2 - (Σy) 2 ))
Onde
- r = coeficiente de correlação
- n = número de observações
- x = 1 r variável no contexto
- y = 2ª variável
Explicação
Se houver alguma correlação ou, digamos, a relação entre duas variáveis, isso deve indicar se uma das variáveis muda de valor, então a outra variável também tende a mudar de valor, digamos em específico que pode ser no mesmo ou em A direção oposta. A parte do numerador da equação conduz um teste e a força relativa das variáveis que se movem juntas, e a parte do denominador da equação dimensiona o numerador multiplicando as diferenças das variáveis das variáveis quadradas.
Exemplos
Exemplo 1
Considere as duas variáveis a seguir, xey, você deve calcular o coeficiente de correlação.
Abaixo estão dados para o cálculo.

Solução:
Usando a equação acima, podemos calcular o seguinte

Temos todos os valores da tabela acima com n = 4.
Vamos agora inserir os valores para o cálculo do coeficiente de correlação.

Portanto, o cálculo é o seguinte,

r = (4 * 25.032,24) - (262,55 * 317,31) / √ ((4 * 20.855,74) - (262,55) 2 ) * ((4 * 30.058,55) - (317,31) 2 )
r = 16.820,21 / 16.831,57
O coeficiente será -

Coeficiente = 0,99932640
Exemplo # 2
O país X é um país de economia em crescimento e deseja realizar uma análise independente das decisões tomadas por seu banco central com relação às mudanças nas taxas de juros, se estas impactaram a inflação e se o banco central tem capacidade de controlá-la.
A seguir, apresenta-se o resumo da taxa de juros e da inflação que prevaleceu no país na média desses anos.
Abaixo estão dados para o cálculo.

O presidente do país o abordou para fazer uma análise e fazer uma apresentação sobre o mesmo na próxima reunião. Use a correlação e determine se o banco central atingiu seu objetivo ou não.
Solução:
Usando a fórmula discutida acima, podemos calcular o coeficiente de correlação. Tratar a taxa de juros como uma variável, digamos x, e tratar a taxa de inflação como outra variável, como y.

Temos todos os valores da tabela acima com n = 6.
Vamos agora inserir os valores para o cálculo do coeficiente de correlação.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
A correlação será -

Correlação = -0,92
Análise: Parece que a correlação entre a taxa de juros e a taxa de inflação é negativa, o que parece ser a relação correta. À medida que a taxa de juros sobe, a inflação diminui, o que significa que tendem a se mover na direção oposta uma da outra, e depreende-se do resultado acima que o banco central foi bem-sucedido na implementação da decisão relacionada à política de taxas de juros.
Exemplo # 3
O laboratório ABC está realizando pesquisas sobre altura e idade e queria saber se existe alguma relação entre eles. Eles reuniram uma amostra de 1000 pessoas para cada uma das categorias e chegaram a uma altura média nesse grupo.
Abaixo estão dados para o cálculo do coeficiente de correlação.

Você deve calcular o coeficiente de correlação e chegar à conclusão de que, se existe alguma relação.
Solução:
Tratando a Idade como uma variável, digamos x, e tratando a altura (em cms) como outra variável, como y.

Temos todos os valores da tabela acima com n = 6.
Vamos agora inserir os valores para o cálculo do coeficiente de correlação.

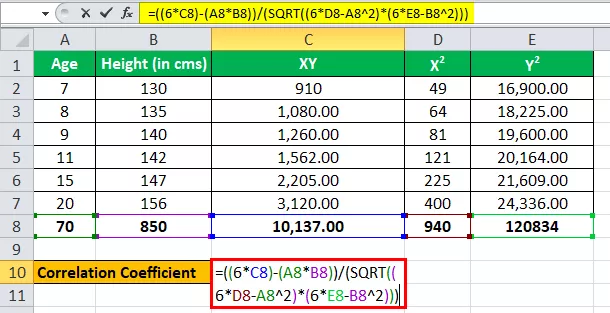
r = (6 * 10.137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1.20.834) - (850) 2 )
r = 1.322,00 / 1.361,23
A correlação será -

Correlação = 0,971177099
Relevância e Uso
É usado em estatística principalmente para analisar a força da relação entre as variáveis que estão sob consideração e, além disso, também mede se há alguma relação linear entre os conjuntos de dados fornecidos e quão bem eles podem estar relacionados. Uma das medidas comuns usadas na correlação é o coeficiente de correlação de Pearson.
Se uma variável muda de valor e, junto com essa outra variável, muda de valor, então entender essa relação é fundamental, pois se pode usar o valor da primeira variável para prever a mudança no valor da última variável. Uma correlação tem muitos usos múltiplos hoje nesta era moderna, como é usada no setor financeiro, na pesquisa científica e onde não é. Porém, é importante saber que a correlação tem três tipos principais de relacionamento. O primeiro é uma relação positiva, que afirma que se houver uma mudança no valor de uma variável, então haverá uma mudança na variável relacionada na mesma direção. Da mesma forma, se houver um relacionamento negativo, a variável relacionada se comportará na direção oposta. Além disso, se não houver correlação, r implicará um valor zero.Veja as imagens abaixo para entender melhor o conceito.









