Definição de Correlação Negativa
Em termos leigos, a correlação negativa é uma relação entre duas variáveis. Eles são parte de uma função na qual variáveis dependentes e independentes se movem em direções diferentes em termos de valor. Por exemplo, se a variável independente aumenta, a variável dependente diminui e vice-versa.
A correlação negativa pode ser descrita pelo coeficiente de correlação quando o valor desta correlação está entre 0 e -1. O valor de uma correlação negativa perfeita é -1. A força da correlação entre as variáveis pode variar. Por exemplo, suponha que duas variáveis, x e y sejam correlacionadas a -0,8. Isso significa que, à medida que x aumenta em 1 unidade, y diminui em 0,8. Agora considere que a correlação negativa entre essas variáveis é -0,1. Nesse caso, cada mudança de unidade no valor da variável x resultará em uma diferença de 0,1 unidade apenas no custo da variável y.
Compreendendo a correlação negativa
Para entender melhor a correlação negativa, também precisamos ter um entendimento básico de correlação. Correlação é uma ferramenta estatística que mede o grau de relação entre duas funções diferentes. Por exemplo, o peso e a altura de uma pessoa. Geralmente, conforme a altura aumenta, o valor da pessoa também aumenta. Isso indica que há uma correlação positiva entre altura e peso porque à medida que uma variável aumenta, outras variáveis também aumentam. Mas a correlação é negativa se as duas variáveis se movem em direções opostas - por exemplo, altura do nível de vedação e temperatura. Conforme a altura aumenta, a temperatura diminui.
A fórmula fornece correlação:

Aqui,
- r = coeficiente de correlação;
- = Média da variável X;
- = Média da variável Y
A reorganização nos dá esta fórmula:

A correlação pode assumir qualquer valor entre -1 e 1. O sinal negativo indica uma correlação negativa, enquanto um sinal positivo indica uma correlação positiva. Correlação zero significa que não há relação entre as duas variáveis.

Por que a correlação negativa é importante?
- Gestão de carteiras : A correlação é amplamente utilizada na gestão de carteiras. Costuma-se dizer que as carteiras devem ser diversas. Deve consistir em vários investimentos envolvendo diferentes riscos e retornos. Se tivermos o mesmo tipo de títulos em nossa carteira, qualquer evento importante afetará não apenas um título, mas toda a carteira. Para tanto, encontramos uma correlação entre os retornos dos títulos. Os depósitos com correlações perfeitamente positivas não devem ser comprados juntos. Para diversificar o portfólio, muitas vezes, as apostas com correlações negativas são adicionadas. Considere o exemplo discutido acima de ações de companhias aéreas e preços do petróleo. Se uma carteira tiver ações de energia, a administração pode considerar a compra de ações de companhias aéreas para se proteger contra a queda nos preços do petróleo.
- Economia : Muitas tendências associadas à economia envolvem correlação negativa. Essa relação entre os movimentos pode ser útil para questões de política econômica. Por exemplo, desemprego e gastos do consumidor. Quanto ao aumento dos gastos, o desemprego diminui (em geral).
Exemplos da vida real de correlação negativa
- Preços do petróleo e ações das companhias aéreas: O petróleo é a principal matéria-prima das companhias aéreas. Conforme os preços do petróleo aumentam, sua lucratividade começa a diminuir, o que se reflete também nos preços de suas ações. Portanto, eles mostram uma correlação negativa
- Mercado de ações e preços do ouro (na maioria das vezes, nem sempre): O ouro sempre atua como uma opção alternativa de investimento para investidores em ações. Assim, sempre que a bolsa parece estar em queda, os investidores se interessam em investir em ouro e, assim, os preços do ouro começam a subir
Exemplo prático de correlação negativa
Suponha que duas ações tenham fornecido os seguintes retornos anualmente no período 2011-16:

Considerando os retornos das ações da primeira ação como variável 'x' e os da segunda ação como 'y'.
Cálculo da variável xy
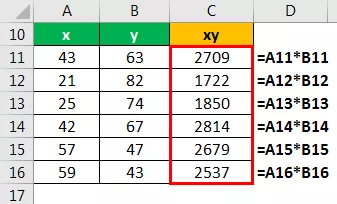
Cálculo da variável X 2

Cálculo da variável Y 2

Soma

Cálculo do coeficiente de correlação (r)

- = ((6 * 14311) - (247 * 376)) / (((6 * 11409) - (247 2)) 0,5 * ((6 * 247160- (376 2)) 0,5)
- = Coeficiente de correlação (r) = -0,97608
Consulte a planilha do excel fornecida acima para cálculos detalhados.
O valor negativo do coeficiente de correlação mostra que as variáveis estão negativamente correlacionadas.
Conclusão
Às vezes, pode haver outros fatores envolvidos que fazem com que as variáveis se comportem de uma maneira particular. No exemplo discutido acima, pode-se deduzir que quando x aumenta, y diminui. Mas será errado supor que o aumento em 'x' está fazendo com que o 'y' diminua porque é possível que ambas as empresas envolvidas estejam envolvidas em negócios totalmente diferentes e sejam afetadas por condições econômicas diferentes.
Portanto, as correlações devem ser usadas apenas para determinar uma causa. Os executivos podem usá-lo para entender a relação entre variáveis, como demanda de mercado e gastos do consumidor, que já existe como parte da análise. Mas não deve ser usado para investigar a mudança em uma variável devido a outras variáveis, porque sempre haverá vários fatores impactando essa relação. Por exemplo, gastos do consumidor no mercado e receita de uma empresa FMCG. Eles podem apresentar uma correlação positiva, mas é possível que a receita dessa empresa tenha aumentado por algum outro motivo, como o lançamento de um novo produto ou a expansão para uma economia emergente.








