Teste Qui-Quadrado com Excel
O teste Qui-quadrado no Excel é o teste não paramétrico mais comumente usado para comparar duas ou mais variáveis para dados selecionados aleatoriamente. É um tipo de teste que é usado para descobrir a relação entre duas ou mais variáveis, isso é usado em estatísticas que também é conhecido como valor de P do qui-quadrado, no Excel não temos uma função embutida, mas podemos usar fórmulas para realizar o teste do qui-quadrado no Excel usando a fórmula matemática do teste do qui-quadrado.
Tipos
- Teste de qui-quadrado para adequação
- Teste do qui-quadrado para independência de duas variáveis.
# 1 - Teste de qui-quadrado para adequação
É usado para perceber a proximidade de uma amostra adequada a uma população. O símbolo do teste Qui-quadrado é (2). É a soma de todas as ( Contagem observada - Contagem esperada) 2 / Contagem esperada.
- Onde k-1 graus de liberdade ou DF.
- Onde Oi é a frequência observada, k é a categoria e Ei é a frequência esperada.
Nota: - A qualidade do ajuste de um modelo estatístico se refere à compreensão de quão bem os dados da amostra se ajustam a um conjunto de observações.
Usos
- A qualidade de crédito dos mutuários com base em suas faixas etárias e empréstimos pessoais
- A relação entre o desempenho dos vendedores e o treinamento recebido
- Retorno sobre uma única ação e sobre ações de um setor como farmacêutico ou bancário
- Categoria de espectadores e o impacto de uma campanha de TV.
# 2 - Teste de qui-quadrado para independência de duas variáveis
É utilizado para verificar se as variáveis são autônomas ou não. Com (r-1) (c-1) graus de liberdade
Onde Oi é a frequência observada, r é o número de linhas, c é o número de colunas e Ei é a frequência esperada
Nota: - Duas variáveis aleatórias são chamadas de independentes se a distribuição de probabilidade de uma variável não é afetada pela outra.Usos
O teste de independência é adequado para as seguintes situações:
- Existe uma variável categórica.
- Existem duas variáveis categóricas e você precisará determinar a relação entre elas.
- Existem tabulações cruzadas e a relação entre duas variáveis categóricas precisa ser encontrada.
- Existem variáveis não quantificáveis (por exemplo, respostas a perguntas como, os funcionários de diferentes faixas etárias escolhem diferentes tipos de planos de saúde?)
Como fazer o teste qui-quadrado no Excel? (com exemplo)
O gerente de um restaurante quer encontrar a relação entre a satisfação do cliente e os salários das pessoas que esperam pelas mesas. Neste, vamos estabelecer a hipótese para testar o qui-quadrado
- Ela pega uma amostra aleatória de 100 clientes perguntando se o serviço foi excelente, bom ou ruim.
- Em seguida, ela categoriza os salários das pessoas que esperam como baixo, médio e alto.
- Suponha que o nível de significância seja 0,05. Aqui, H0 e H1 denotam a independência e dependência da qualidade do serviço em relação aos salários das pessoas que servem à mesa.
- H 0 - a qualidade do serviço não depende do salário de quem espera nas mesas.
- H 1 - a qualidade do serviço depende do salário de quem espera nas mesas.
- Suas descobertas são mostradas na tabela abaixo:
Neste, temos 9 pontos de dados, temos 3 grupos, cada um dos quais recebeu uma mensagem diferente sobre o salário, e o resultado é dado abaixo.

Agora vamos contar a soma de todas as linhas e colunas. Faremos isso com a ajuda da fórmula, ou seja, SUM. Para totalizar o excelente na coluna total, escrevemos = SUM (B4: D4) e, em seguida, pressione a tecla Enter.

Isso nos dará 26 . Faremos o mesmo com todas as linhas e colunas.

Para calcular o Grau de Liberdade (DF), usamos (r-1) (c-1)
DF = (3-1) (3-1) = 2 * 2 = 4
- Existem 3 categorias de serviço e 3 categorias de salário.
- Temos 27 entrevistados com salário médio (linha inferior, meio)
- Temos 51 entrevistados com um bom atendimento (última coluna, meio)
Agora temos que calcular as frequências esperadas: -
As frequências esperadas podem ser calculadas usando uma fórmula: -
- Para calcular o Excelente, usaremos a multiplicação do total de Baixo pelo total de Excelente dividido por N.
Suponha que tenhamos que calcular para a 1ª linha e 1ª coluna (= B7 * E4 / B9 ) . Isso dará o número esperado de clientes que votaram no serviço Excelente para os salários das pessoas que aguardam tão baixos, ou seja, 8,32 .
- E 11 = - (32 * 26) / 100 = 8,32 , E 12 = 7,02 , E 13 = 10,66
- E 21 = 16,32 , E 22 = 13,77 , E 23 = 20,91
- E 31 = 7,36 , E 32 = 6,21 , E 33 = 9,41
Da mesma forma, para todos, temos que fazer o mesmo, e a fórmula é aplicada no diagrama abaixo.

Obtemos a tabela de frequência esperada conforme abaixo: -

Nota: - Suponha que o nível de significância seja 0,05. Aqui, H0 e H1 denotam a independência e dependência da qualidade do serviço em relação aos salários das pessoas que servem à mesa.
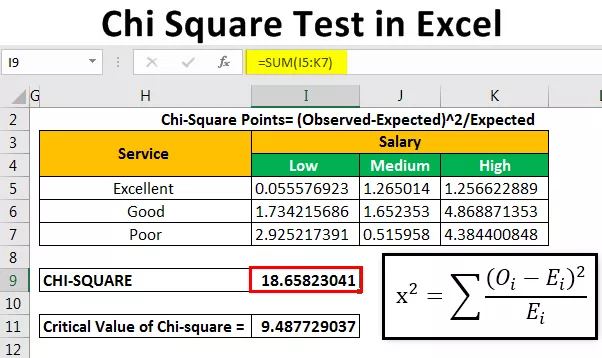
Depois de calcular a frequência esperada, calcularemos os pontos de dados qui-quadrado usando uma fórmula.
Pontos Qui-Quadrado = (Observado-Esperado) 2 / Esperado
Para calcular o primeiro ponto, escrevemos = (B4-B14) 2 / B14.

Vamos copiar e colar a fórmula em outras células para preencher o valor automaticamente.

Depois disso, calcularemos o valor chi (valor calculado) adicionando todos os valores dados acima da tabela.

Obtivemos o valor de Chi de 18,65823 .

Para calcular o valor crítico para isso, usamos uma tabela de valores críticos do qui-quadrado de podemos usar a fórmula fornecida abaixo.
Esta fórmula contém 2 parâmetros CHISQ.INV.RT (probabilidade, grau de liberdade).
A probabilidade é 0,05 e é um valor significativo que nos ajudará a determinar se devemos aceitar a hipótese nula (H 0 ) ou não.

O valor crítico do qui-quadrado é 9,487729037.

Agora encontraremos o valor do qui-quadrado ou (valor P) = CHITEST (intervalo_real, intervalo_esperado)
Faixa de = CHITEST (B4: D6, B14: D16) .

Como vimos, o valor do teste do qui ou valor P é = 0,00091723.

Calculamos todos os valores. Os valores do qui-quadrado (valor calculado) só são significativos quando seu valor for igual ou maior que o valor crítico 9,48, ou seja, o valor crítico (valor tabulado) deve ser maior que 18,65 para aceitar a hipótese nula (H 0 ) .
Mas aqui valor calculado > valor tabulado
X 2 (Calculado)> X 2 (Tabulado)
18,65> 9,48
Neste caso, rejeitaremos a Hipótese Nula (H 0 ), e a Alternativa (H 1 ) será aceita.
- Também podemos usar o valor P para prever o mesmo, ou seja, se o valor P <= α (valor significativo 0,05), a hipótese nula será rejeitada.
- Se o valor P> α , não rejeite a hipótese nula .
Aqui o valor P (0,0009172) < α (0,05), rejeita H 0 , aceita H 1
Do exemplo acima, concluímos que a qualidade do serviço depende dos salários das pessoas que esperam.
Coisas para lembrar
- Considera o quadrado de uma variável normal padrão.
- Avalia se as frequências observadas em diferentes categorias variam significativamente em relação às frequências esperadas sob um conjunto específico de premissas.
- Determina o quão bem uma distribuição assumida se ajusta aos dados.
- Usa tabelas de contingência (em pesquisas de mercado, essas tabelas são chamadas de tabulações cruzadas).
- Ele suporta medições de nível nominal.








