Definição do Método de Regressão de Mínimos Quadrados
Um método de regressão de mínimos quadrados é uma forma de análise de regressão que estabelece a relação entre a variável dependente e independente junto com uma linha linear. Esta linha é conhecida como a "linha de melhor ajuste".
A Análise de Regressão é um método estatístico com o qual se pode estimar ou prever os valores desconhecidos de uma variável a partir dos valores conhecidos de outra variável. A variável que é usada para prever o interesse variável é chamada de variável independente ou explicativa, e a variável que está sendo prevista é chamada de variável dependente ou explicada.
Vamos considerar duas variáveis, x e y. Eles são plotados em um gráfico com valores de x nos valores do eixo x de y no eixo y. Esses valores são representados pelos pontos no gráfico abaixo. Uma linha reta é desenhada através dos pontos - referida como a linha de melhor ajuste.

O objetivo da regressão de mínimos quadrados é garantir que a linha traçada através do conjunto de valores fornecidos estabeleça a relação mais próxima entre os valores.
Fórmula de regressão de mínimos quadrados
A linha de regressão no método dos mínimos quadrados é calculada usando a seguinte fórmula -
ŷ = a + bx
Onde,
- ŷ = variável dependente
- x = variável independente
- a = interceptação y
- b = inclinação da linha
A inclinação da linha b é calculada usando a seguinte fórmula -

Ou

Interceptação Y, 'a' é calculado usando a seguinte fórmula -

Linha de melhor ajuste na regressão do mínimo quadrado
A linha de melhor ajuste é uma linha reta desenhada através de uma dispersão de pontos de dados que melhor representa a relação entre eles.
Vamos considerar o gráfico a seguir, no qual um conjunto de dados é plotado ao longo dos eixos xey. Esses pontos de dados são representados por pontos azuis. Três linhas são traçadas por esses pontos - uma verde, uma vermelha e uma azul. A linha verde passa por um único ponto e a linha vermelha passa por três pontos de dados. No entanto, a linha azul passa por quatro pontos de dados e a distância entre os pontos residuais até a linha azul é mínima em comparação com as outras duas linhas.

No gráfico acima, a linha azul representa a linha de melhor ajuste, pois está mais próxima de todos os valores e a distância entre os pontos fora da linha até a linha é mínima (ou seja, a distância entre os resíduos até a linha de melhor ajuste - também conhecido como a soma dos quadrados dos resíduos). Nas outras duas linhas, a laranja e a verde, a distância entre os resíduos às linhas é maior em comparação à linha azul.
O método dos mínimos quadrados fornece a relação mais próxima entre as variáveis dependentes e independentes, minimizando a distância entre os resíduos e a linha de melhor ajuste, ou seja, a soma dos quadrados dos resíduos é mínima sob esta abordagem. Daí o termo “mínimos quadrados”.
Exemplos de linhas de regressão de mínimos quadrados
Vamos aplicar essas fórmulas na pergunta abaixo -
Exemplo 1
Os detalhes relativos à experiência dos técnicos em uma empresa (em vários anos) e sua classificação de desempenho são fornecidos na tabela abaixo. Usando esses valores, estime a classificação de desempenho para um técnico com 20 anos de experiência.
| Experiência de técnico (em anos) | Avaliação de Desempenho |
| 16 | 87 |
| 12 | 88 |
| 18 | 89 |
| 4 | 68 |
| 3 | 78 |
| 10 | 80 |
| 5 | 75 |
| 12 | 83 |
Solução -
Para calcular os quadrados mínimos primeiro, calcularemos a interceptação Y (a) e a inclinação de uma linha (b) da seguinte forma -

A inclinação da linha (b)

- b = 6727 - ((80 * 648) / 8) / 1018 - ((80) 2 /8)
- = 247/218
- = 1,13
Interceptação Y (a)

- a = 648 - (1,13) (80) / 8
- = 69,7
A linha de regressão é calculada da seguinte forma -

Substituindo 20 pelo valor de x na fórmula,
- ŷ = a + bx
- ŷ = 69,7 + (1,13) (20)
- ŷ = 92,3
A classificação de desempenho para um técnico com 20 anos de experiência é estimada em 92,3.
Exemplo # 2
Equação de regressão de mínimos quadrados usando Excel
A equação de regressão de mínimos quadrados pode ser calculada usando o Excel pelas seguintes etapas -
- Insira a tabela de dados no excel.

- Insira um gráfico de dispersão usando os pontos de dados.

- Insira uma linha de tendência no gráfico de dispersão.

- Nas opções de linha de tendência - selecione a linha de tendência linear e selecione a equação de exibição no gráfico.

- A equação de regressão de mínimos quadrados para o determinado conjunto de dados do Excel é exibida no gráfico.
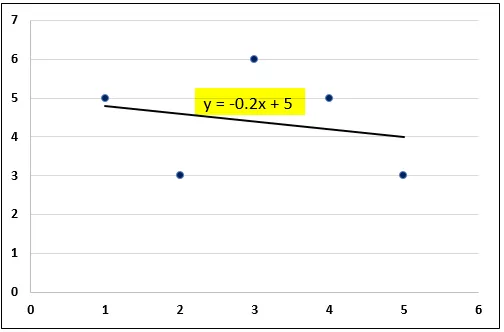
Assim, a equação de regressão de mínimos quadrados para o conjunto de dados do Excel fornecido é calculada. Usando a equação, previsões e análises de tendência podem ser feitas. As ferramentas do Excel também fornecem cálculos de regressão detalhados.
Vantagens
- O método dos mínimos quadrados de análise de regressão é mais adequado para modelos de previsão e análise de tendência. É mais bem usado nas áreas de economia, finanças e mercados de ações, em que o valor de qualquer variável futura é previsto com a ajuda de variáveis existentes e a relação entre as mesmas.
- O método dos mínimos quadrados fornece a relação mais próxima entre as variáveis. A diferença entre as somas dos quadrados dos resíduos para a linha de melhor ajuste é mínima com este método.
- O mecanismo de computação é simples e fácil de aplicar.
Desvantagens
- O método dos mínimos quadrados baseia-se no estabelecimento da relação mais próxima entre um determinado conjunto de variáveis. O mecanismo de cálculo é sensível aos dados e, no caso de quaisquer outliers (dados excepcionais), os resultados podem tender a afetar de forma significativa.
- Este tipo de cálculo é mais adequado para modelos lineares. Para equações não lineares, mecanismos de computação mais exaustivos são aplicados.
Conclusão
O método dos mínimos quadrados é um dos métodos mais popularmente usados para modelos de previsão e análise de tendências. Quando calculado de forma adequada, ele fornece os melhores resultados.








