O que é Dietz modificado?
Dietz modificado refere-se à medida que é usada para determinar o desempenho histórico da carteira, dividindo o fluxo de caixa real líquido da saída pelo capital médio, que usa o peso e o valor da carteira no início. Em um método Dietz simples, todos os fluxos de caixa são assumidos como provenientes do meio do período, ao passo que esse não é o caso com o método Dietz modificado.
Fórmula
A taxa de retorno de Dietz modificada pode ser definida usando a seguinte fórmula e cada um dos termos nela explicados:
ROR = (EMV - BMV - C) / (BMV + W * C)
- ROR (Taxa de Retorno) - este é o termo que procuramos calcular
- EMV (Ending Market Value) - É o valor da carteira após o final do prazo que procuramos.
- BMV (Valor de Mercado Inicial) - É o valor da carteira a partir da data em que os retornos serão calculados
- W (Peso de cada fluxo de caixa na carteira) - É o peso da carteira entre zero e um, mas apenas entre o período em que ocorreram e no final do período. Isso pode ser explicado como a proporção de tempo entre o momento em que ocorre o fluxo e o final do período. Isso pode ser calculado usando a fórmula.
- W = (C- D) / C onde D é o número de dias desde o início do período de retorno até o dia em que ocorreu o fluxo.
- C - Fluxos de caixa durante o período - pode não ser um único número, mas uma série de fluxos de caixa que aconteceram durante o período.
- W * C = soma de cada fluxo de caixa multiplicada por seu peso. Este é um somatório dos fluxos de caixa ponderados.
Exemplos
Abaixo estão alguns exemplos do método Dietz modificado.
Exemplo 1
Vamos considerar um cenário muito simples com as seguintes condições:
- Temos uma carteira de US $ 1 milhão no início do período de investimento.
- Após dois anos, o valor da carteira cresceu para 2,3 milhões de dólares.
- Houve uma entrada de 0,5 milhões de dólares após um ano.
Agora, vamos calcular como o método Dietz Modificado será usado para calcular os retornos desta carteira.

- Lucro real = EMV (2,3 milhões de dólares) - BMV (1 milhão de dólares) - Fluxos de caixa (0,5 milhões de dólares de entrada)
- = $ 0,8
Isso traz um lucro de 0,8 milhões de dólares.
Agora vamos ver qual foi o capital médio neste caso.

- Capital médio = BMV (1 milhão de dólares) + W * C (0,5 milhões de dólares * 0,5 período de tempo)
- = 1,25
Portanto, a taxa de retorno será -
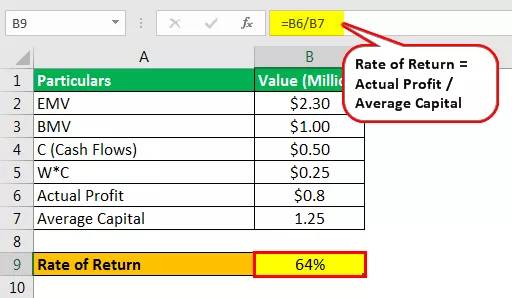
- Taxa de retorno = lucro real / capital médio
- = $ 0,8 / 1,25
- = 64%
Exemplo # 2
Comparação de Dietz modificado com taxa de retorno ponderada pelo tempo
Vamos considerar dois investidores com as seguintes carteiras.
- O Investidor A começou com uma carteira de 250k USD no início de um ano (Jan) e utilizou as suas estratégias para chegar a 298k USD no final do mesmo ano (Dez). No entanto, ele colocou um capital adicional de 25k USD em setembro.
- O Investidor B começou com uma carteira de 250k USD no início do ano (Janeiro) e utilizou as suas estratégias mas acabou com 2 51k USD no final do ano. No entanto, ele retirou 25K em setembro.
A olho nu, ou usando matemática elementar em nossas mentes, podemos dizer que o Investidor B é ruim em investir do que o investidor A. No entanto, ir fundo nos cálculos nos dará um outro lado da história inteiramente.
Para o Investidor A:
O lucro real será -

- Lucro real = (298 mil USD - 250 mil USD - 25 mil USD)
- = 23K USD
O período médio será -

- Período médio = 250k USD + (25k USD * 0,3)
- = 258K USD
A taxa Dietz modificada será -

- Taxa Dietz modificada = 8,7%
Para o Investidor B:
O lucro real será -
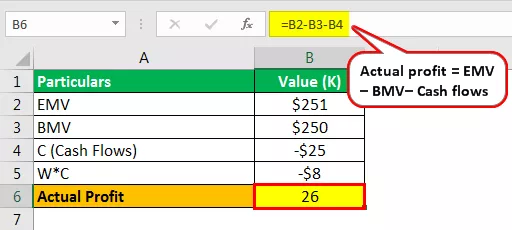
- Lucro real = (251k USD - 250k USD + 25k USD)
- = 26K USD
O período médio será -

- Período médio = 250k USD + (-25K USD * 0,3)
- = 242,5 k USD
A taxa Dietz modificada será -

- Taxa Dietz modificada = 10,72%
A taxa de retorno ponderada pelo tempo para ambos os itens acima será em torno de 9,5, mas Dietz modificado nos deu resultados diferentes. Esta é a razão pela qual este método é usado pelos investidores para fins de relatório.
Vantagens
- A principal vantagem desse método é que ele não requer avaliação do portfólio em cada data do fluxo de caixa. Isso ajuda o analista a afirmar o valor dos retornos facilmente, sem reavaliar a cada vez.
- Existem atribuições de desempenho que não estão disponíveis com outros métodos de ponderação de tempo; durante esses casos, o método Dietz modificado é útil.
- Casos como o Exemplo 2, em que a Taxa de Retornos Ponderada pelo Tempo não é uma medida apropriada.
Limitações
- Com o avanço da computação, a maior parte dos retornos de hoje são calculados de forma contínua - fornecem uma maneira melhor de analisar os retornos e deixam métodos como o Dietz modificado muito ingênuo e básico.
- A suposição de que todas as transações ocorram simultaneamente em um único ponto de um período de tempo levará a erros.
- É muito difícil lidar com fluxos de caixa negativos ou com média zero.
Conclusão
À medida que as regulamentações em torno do setor financeiro crescem, os investidores precisam tomar mais cuidado com a forma como o investimento e os retornos são calculados e como são relatados. Este método de Dietz modificado fornece confiança razoável na análise de retorno de investimento.
O método Dietz modificado apenas nos fornece uma medida de retorno sobre carteiras de investimento, onde há várias entradas e saídas. Nos dias atuais, com computação avançada e gerenciamento contínuo de devoluções, esse método não é útil. No entanto, o conceito básico por trás do método é útil para entender como funcionam os retornos e seus cálculos.








